Google Apps Scriptでソルバーを実現する【GAS】
Google Apps Scriptの中で殆どの人が使ったことがないであろう特殊なクラスがあります。それがLinear Optimization Service。ひとことで言えばExcelのソルバー機能をAPIにしたもの。といってもソルバー自体殆どの人が使ったことが無いでしょう。
このソルバーは線形計画法と呼ばれるもので、様々な条件満たし制約事項をクリアした組み合わせを導くもので、限られた予算で複数種類のものを何個ずつ買えるか?であったり、アルバイトのシフト組みなどで利用されていたりします。
今回はこれにチャレンジしてみたいと思います。
目次
今回利用するファイル
- 線形計画法でバイトシフト組み - Google Spreadsheet
- Class LinearOptimizationService
メソッドそのものは極端に複雑というわけではないのですが、自分自身も数学はとても苦手で・・・数学の理論を用いてる為、メソッドよりもその仕組や流れを理解することに多くの時間を割くことになります。このクラスを手軽に使えるようにしたSolverというSpreadsheetアドオンも出ていたりするのですが、英語しか無いので使いにくいです。
よって自前で装備出来るようにしたいのが今回の目的。ただ、ウェブでも殆ど事例が無く・・・・
今回は指定の日数分、シフトパターン、1日のメンバー数、演算するメンバーにてアルバイトのシフトを組んでみるという演算をやらせています。制約条件をあまりキツくしていません。
そもそも線形計画法とは何か?
概要
線形計画法と聞くと蕁麻疹が出ますが、実のところ身近なところでこの考えは皆が利用していたりします。例えば日々の買い物に於いて
- 予算という名の制約条件を設定(例えば1000円など)
- 購入する商品A(例えば100円)を「𝑥」とする(数式だと100𝑥となる)
- 購入する商品B(例えば50円)を「𝑦」とする(数式だと50𝑦となる)
- このAとBを組み合わせて、1000円で買えるだけ買うということならば、100𝑥 + 50𝑦 = 1000ということになる
- この数式を満たすAとBの組み合わせのパターンを算出して調べるのが線形計画法ということになります。
- ここにさらにA商品は最低2個以上であったり、B商品は10個未満といったような追加の制約条件を加えて絞り込むことになります(たとえば、)
- もちろん制約条件が厳しすぎて解が見つからないということもあります。
同じような考え方で、複数名のアルバイトについて、月間の出勤日数という制約条件(バイト枠)を設定し、それぞれが週に何回出勤するか?といった組み合わせのパターンを算出することで、要件を満たすシフトを組めるといったことになります。
但し前述の中にもあるように、個々の人間の細かすぎる要件を全部盛り込んでも解答が得られる魔法のステッキではありません。それは要件がどんどん厳しくしてることに他ならない為注意しましょう。
LinearOptimizationについて
Google Apps Scriptに於いて、LinearOptimization Serviceの各種メソッドは非常に独特であり、中身を理解できていないと一体何をやってるのやらさっぱりわかりません。今回のサンプルではアルバイトのシフト組みというシーンで利用していますが、これがショッピングに於いて組み合わせで購入できるものを調べるなんてパターンだと書き方が大分変わってきます。
LinearOptimizationService.createEngine()で作成したエンジンに対して以降の項目にあるような内容をセットしていくことになります。
変数名
今回のサンプルでは、日付・シフトパターン・メンバーという3要素がキーになります。これら3次元の要素を元に演算するわけですが、それぞれに対して全部変数を一気に用意する必要があり、その変数に重複しない名前付けが必要になります。
そこでvariable関数を用意し、それぞれのループの変数の値を持ってして自動的に構築するように構築します。x, j, vの3つの要素なので、1つ目の変数であればその変数名は「x_1_1_1」という名称が返されます。
この変数は後の工程での制約条件や目的関数でも利用することになります。変数名で特定してセットすることになるので、地味ですが重要な関数です。今回の条件指定では合計84個の変数がこれで用意されることになります(7日 * 3パターン * 4名)
変数の登録
演算で利用する変数を前述のvariable関数で変数名を生成し、必要な分だけ登録していくのが変数の登録作業です。
engine.addVariable(vari,0,1, LinearOptimizationService.VariableType.INTEGER)
- variには生成した変数名が入ります。
- 次の引数の0は今回はオンオフで表現するので、下限値の0を入れます
- 次の引数の1は今回はオンオフで表現するので、上限値の1を入れます
- 変数の型指定として、Integerを指定しています。
これを84個分繰り返す為に3重ループを構築して、engineに対して生成しています。
※例えば商品の組み合わせパターンで演算といったような場合には、ここは個数などが入ることになるので、下限値は0として上限値は例えば100などを指定することになります。但し制約要件の内容の影響を受けることになりますので、100と指定しても制約で50であればここにその変数に対して100が入ることはありません。
制約条件の追加
今回のサービスに於いて、一番重要なポイントがこの制約条件の追加。今回のサンプルでは1日のシフトメンバー数と各メンバーの出勤回数の2つが制約条件となります。よってコードの中では、下限値と上限値の2つを定義し変数に対してセットすることになります。
//最小値と最大値のセット let constraint = engine.addConstraint(最小値,最大値); //変数にセットする constraint.setCoefficient(vari,最大値);
addConstraintにて対象の変数に対する制約値に於いて取りうる最大値と最小値をセットします。そして、setCoefficientにて変数にセットします。この時の引数には変数名と取りうる最大値を入れておきます。
x, y, vのそれぞれの項目に対してどう制約を加えていくか?がポイントになり、多ければ多いほど条件が厳しくなり解が得られにくくなるので、加え方についてはよく設計して追加する必要があります。
目的関数の追加
目的関数とは、実行前にセットする「最小化」「最大化」に合わせてセットするもので、setObjectiveCoefficientメソッドにて変数名と係数を指定します。
engine.setObjectiveCoefficient(vari,1)
この係数は通常は取りうる値の最大値を指定します。
今回の演算では、出勤するか?しないか?の2つしか無いため、0か1となる。よって、ここでは係数は1を指定します。買い物の組み合わせならば各商品の単価を入れることになります(xやyの値の取り得る値の最大値)。
そして最後に最大化?最小化?を求める為に以下のようなメソッドで指定します。
//最小化 engine.setMinimization(); //最大化 engine.setMaxmization();
制約をクリアした上での取りうる値で最小のパターンや最大のパターン、それぞれに合わせて上記のどちらかをセットすることになります。今回のケースではどちらを使っても解答に変わりはありません。
演算の実行と解答
各種変数、制約条件、目的関数、最小最大化の指定が完了したら、いよいよ演算実行になります。この演算結果をまたループで2次元配列として格納し直し、スプレッドシートに一括で書き込むことになります。
//演算の実行 let result = engine.solve(); //結果から変数名指定で値を取り出す let assign = result.getVariableValue(vari);
今回のケースでは、0で休み、1で出勤という形で値が返ってきます。これを後の処理でfalse/trueに変換して返すようにしています。
ソースコード等
各種条件
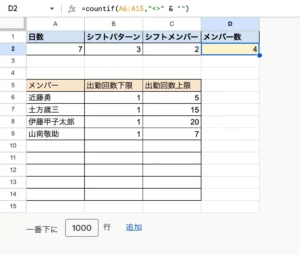
今回の課題では、以下のような条件を設定して実行したら、シフト組みが成功しました。各条件の値を変更したり、メンバーを増やすことで解が出なくなる可能性も多分にあります。
- 日数は1週間分
- 1日のシフトパターンは朝・昼・夕の3パターン
- 1日のシフトメンバーは2名まで
- シフト組みするメンバーは4名
- 各メンバーの出勤回数の上下限値は適当にセットしていますが、ここの制約の付け方で大分変わります。
また、実際の現場で利用するには、これだけでは制約条件は足りないと思います(例えば、週に出勤する日数の制約であったり、連続稼働制約、会社の休日制約、熟練度レベル、雇用形態などなど。これらを追加の制約要件として盛り込む必要があります。
※病院の看護師さんや薬剤師さんの勤務表などは法的に求められる配置基準というものがあるため、こういったソルバーを使って、対象の日のメンバー更生が配置基準を満たしてるかどうか?などの用途としても利用できるのではないかと思います。
図:今回設定した各種条件
コード
//変数定義用
function variable(i, j, v) {
//値調整(1から始まるように調整)
i = i + 1;
j = j + 1;
v = v + 1;
//変数返却
return "x_" + i + "_" + j + "_" + v;
}
//シフト生成ルーチン
function generateShift(){
//スプシを取得する
let ui = SpreadsheetApp.getUi();
let sheet = SpreadsheetApp.getActiveSpreadsheet().getSheetByName("data");
let values = sheet.getRange("A2:D").getValues();
//パラメータをセットする
let days = values[0][0]; //シフト日数
let shiftptn = values[0][1]; //シフトパターン
let memnum = values[0][2]; //1シフトの固定メンバー数
let members = values[0][3]; //全メンバー数
//memnumに基づいて各シフトのメンバー数を配列に指定(今回は全部固定)
let shiftman = [memnum,memnum,memnum]
//メンバーデータを取得する
let attend = sheet.getRange("A6:C").getValues();
//シフト組みを実行
let result = doOptimize(days,shiftptn,members,shiftman,attend);
//エラートラップ
if(result == 0){
ui.alert("💀 解が見つかりませんでした。\n再度パラメータを定義し直して実行してください。")
return;
}
//取得した結果を一括で書き出し
let editsheet = SpreadsheetApp.getActiveSpreadsheet().getSheetByName("shift");
editsheet.getRange("C3:AC").clearContent();
let lastColumn = result[0].length; //カラムの数を取得する
let lastRow = result.length; //行の数を取得する
editsheet.getRange(3,3,lastRow,lastColumn).setValues(result);
//終了処理
ui.alert("演算が終了しました。")
}
//線形計画実行関数
function doOptimize(days,shiftptn,members,shiftman,attend){
//エンジン生成
let engine = LinearOptimizationService.createEngine();
//変数登録をする
//i = 日付, j = シフト, v = アルバイト
for(let i=0; i<days; i++){
for(let j=0; j<shiftptn;j++){
for(let v=0; v<members; v++){
//変数を用意
let vari = variable(i,j,v)
//変数を追加
engine.addVariable(vari,0,1, LinearOptimizationService.VariableType.INTEGER)
}
}
}
//制約条件を登録する
//シフトメンバー数の制約(今回は固定値)
for(let i=0; i<days; i++){
for(let j=0; j<shiftptn;j++){
//制約を追加(固定値)
let constraint = engine.addConstraint(shiftman[j],shiftman[j]);
for(let v=0; v<members; v++){
//変数を用意
let vari = variable(i,j,v);
//メンバー人数ごとの制約を追加
constraint.setCoefficient(vari,1);
}
}
}
//出勤回数の制約
for(let v=0; v<members; v++){
//制約を追加(下限値と上限値を指定)
let constraint = engine.addConstraint(attend[v][1],attend[v][2]);
for(let i=0; i<days; i++){
for(let j=0; j<shiftptn;j++){
//変数を用意
let vari = variable(i,j,v);
//シフト日毎の制約を追加
constraint.setCoefficient(vari,1);
}
}
}
//目的関数の登録
for(let i=0; i<days; i++){
for(let j=0; j<shiftptn;j++){
for(let v=0; v<members; v++){
//変数を用意
let vari = variable(i,j,v)
//変数を追加
engine.setObjectiveCoefficient(vari,1)
}
}
}
//最小の値で算出する
engine.setMinimization();
//エンジンの実行
let result = engine.solve();
//演算結果を取得する
let assignment = [];
if(result.isValid()){
//解があった場合
for(let i=0; i<days; i++){
//日割当用一時変数
let dayassign = [];
for(let j=0; j<shiftptn;j++){
for(let v=0; v<members; v++){
//変数を用意
let vari = variable(i,j,v)
//変数を追加
let assign = result.getVariableValue(vari);
//チェックボックス用に返還
if(assign == 0){
assign = false;
}else{
assign = true;
}
//日割当変数に追加
dayassign.push(assign);
}
}
//asignmentに追加
assignment.push(dayassign);
}
//解を返却
return assignment;
}else{
//解が無い場合
return 0;
}
}
- メインの関数はgenerateShift関数ですが、その中でdoOptimizeを呼び出しています
- 実際に線形計画法にて各種条件設定や算出を行ってるのはdoOptimize関数で、解が無い場合には0を返し、解がある場合は配列データで返します。
- 返却される配列データは1レコードにメンバー分の朝・昼・夕の出る出ないのオンオフを格納(計算式でtrue/falseに変換しています)
- 変数の追加時は0〜1の値とし、値はIntegerで追加するようにしています(setAddVariable)。
- 故に各変数のCofficientの引数には変数名と1をセットしています(1より上の値が来ても困る)
- 今回は最低限の組み合わせとしてるため、実行はsetMinimizationとしています。メンバーの数や日数、制約要件によってここがsetMaxmizationにする必要があります。
- variable関数は変数名を定義しますが、必ず1から始まるように調整を掛けています。
- 今回は1日のシフトメンバー数は朝昼夕それぞれ2名で固定化しています。
実行結果
算出した結果は配列で返ってくるのと同時に、中の値は0,1ではなく、false,trueとして変換しています。これはチェックボックスのオンオフで表現する為にこのようにしています。チェックがある場所が出勤するシフトになります。毎回、このチェックボックス値は実行前にクリアされます。
メンバーの名前や日付、曜日なども生成時に自動的にセットするような処理もあると尚良いかなと思います(今回はあくまでLinearOptimizationの結果だけを貼り付けている)。
図:チェックボックスのオンオフで表現
考察
ここまで見てもわかるように、非常に数学的な思考と理解が必要になるため、なかなか使いこなすというのが難しいメソッドになります。極簡単な制約事項でもって今回は結果を出してる為、わりと計算しやすいのですが、冒頭にもあったようにこれでは制約条件は実際には足りないと思います。
また出勤するかしないか?の2択の問題であるため、最大値・最小値の設定も比較的シンプルですが、買い物のような組み合わせの場合には、x, y, v以外にもさらに要素が増えるので、コードの組み方も変わってくると思います。
また、最近はこの手の演算に関しては、Claude 3.5 Sonnetのような生成AIでもシフト表を組めるようになったようなので、理解の難しいこのクラスを使わずに生成AIにぶんなげて答えを得るというテクニックでも実現できるのではないかと思います。
関連リンク
- Apps Script の LinearOptimizationService で数独を解く
- 「ファミマ 5days チャレンジ」の舞台裏
- GOOGLE APP SCRIPT - LinearOptimizationService - Minimization of absolute deltas - Problem Infeasible
- Ranges are not passed as 2DArrays to Custom function
- Solver - Google Workspace Marketplace
- Excel(エクセル)のCOUNTIF関数の使い方!複数条件や空白以外のセルをカウントする方法
- Googleスプレッドシートで曜日を自動入力する方法
- Googleの数理最適化ツールOR-Toolsを使ってみる
- Google scripts optimization